2D crystallographic symmetry is a way of describing patterns of symmetry in two-dimensional crystalline structures. A crystalline is a solid material with a highly ordered microscopic structure.

At a larger scale, crystalline structures could also be tiles or wallpapers – patterns that repeat in a plane, maintaining its structure and orientation. In 2D, symmetry operations include translations, rotations, reflections, and glide reflections. Only specific combinations of these operations are allowed to create repeating patterns that fill the plane. There are exactly 17 distinct plane symmetry groups (image below), known as wallpaper groups, that classify all possible 2D repeating patterns.
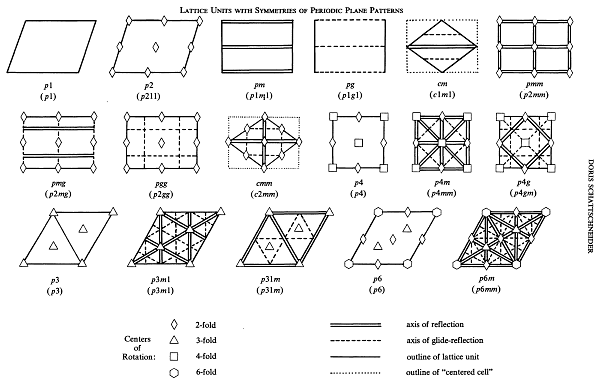
Each group has a unique combination of symmetry operations. These symmetry types help in categorizing various natural and artificial patterns, such as honeycombs or mosaics. Studying 2D crystallographic symmetry is fundamental in fields like crystallography and materials science.
Additional supporting concepts I learned:
- Bilayer graphene – need to study further later. probably more in chemistry side.
- Invariant –
- Tychonoff space
- Topological space
- Separation axiom
- Hausdorff space
- Homomorphism